Table of Contents
Applications and Performances
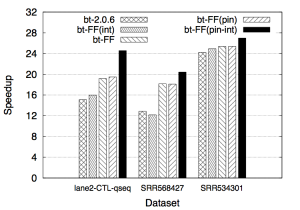
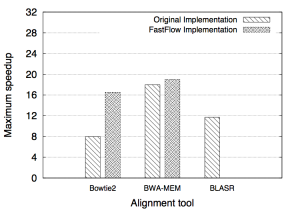
[2014] NGS tools (Bowtie2, BWA)
Bowtie2.0.6, Bowtie-2.2.1, and BWA compared in performance against their porting onto the FastFlow library. Tested on
- Intel 4-socket 8-core Nehalem (64 HT) @2.0GHz, 72MB L3, 64 GB mem, Linux x86_64
- Intel 2-socket 8-core Sandy Bridge (32 HT) @2.2GHz, 40MB L3, 64 GB mem, Linux x86_64
More details in:
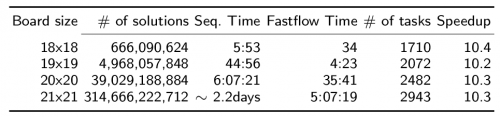
- C. Misale, “Accelerating Bowtie2 with a lock-less concurrency approach and memory affinity,” in Proc. of Intl. Euromicro PDP 2014: Parallel Distributed and network-based Processing, Torino, Italy, 2014. doi:10.1109/PDP.2014.50 PDF
- C. Misale, G. Ferrero, M. Torquati, and M. Aldinucci, “Sequence alignment tools: one parallel pattern to rule them all?,” BioMed Research International, 2014. doi:10.1155/2014/539410 PDF
[2012] Yadt-ff (parallel C4.5)
The well-known C4.5 statistical classifier is a double hard algorithm. First of all, because data-miners simply would not like to spend time on a yet another brand new parallel version ![]() Many past experiences demonstrated that tiny improvements of the sequential algorithm could bring much more performance than a robust investment on parallelization. This clearly does not absolutely mean that parallelization is useless, but, at least in our understanding, that a low-effort and conservative parallelization is the only fairly welcome parallelization in the data-mining community. Unfortunately that kind of parallelization, i.e. loop and recursion parallelization, is technically complex because independent tasks generated in this way may exhibit several non nice proprieties, including a huge range of variability in the task size that in turn may induce both severe synchronization overheads and non-trivial load balancing problems that limit the speedup.
Many past experiences demonstrated that tiny improvements of the sequential algorithm could bring much more performance than a robust investment on parallelization. This clearly does not absolutely mean that parallelization is useless, but, at least in our understanding, that a low-effort and conservative parallelization is the only fairly welcome parallelization in the data-mining community. Unfortunately that kind of parallelization, i.e. loop and recursion parallelization, is technically complex because independent tasks generated in this way may exhibit several non nice proprieties, including a huge range of variability in the task size that in turn may induce both severe synchronization overheads and non-trivial load balancing problems that limit the speedup.
The YaDT-FastFlow application faces both problems. YaDT is a third-party, main-memory implementation of the C4.5-like decision tree algorithm by Salvatore Ruggieri. YaDT-FastFlow is a low-effort parallelization of the sequential algorithm that required less than 10 hours of development (including tuning and testing) while producing a significant speedup over the sequential version.
This application aims at demonstrating the ability of FastFlow and FastFlow accelerator to support rapid and efficient development via semi-automatic parallelization of loops and Divide&Conquer in third-party and legacy codes.
Stay tuned for a brand new Technical Report about that. The code will be publicly available with the Technical Report. The C.4.5-FastFlow application has been developed in cooperation with Salvatore Ruggieri, University of Pisa, Italy.
Performances
Tests on andromeda (2 x quad-core HT - 16 contexts, Linux) and ottavinareale (2 x quad-core, Linux).
We have been developing several applications using FastFlow and FastFlow accelerator. The complexity of them ranges from simple micro-benchmarks to quite complex scientific and business applications. Clearly, our main business consists in developing FastFlow itself more than any big or complex application. However, we believe that developing and running applications is the only effective way to demonstrate that FastFlow is a viable and convenient way to high-level parallel programming for multi-core. For this, each application is carefully chosen in order to demonstrate a particular aspect of feature of FastFlow, and we try make them timeliness available to third-parties with all the information needed to understand the code and reproduce the experiments we did. We also try to publish a Technical Report for each significant advance. Said that, we are also very interested to support independent programmers, scientists, and industries that would like to try FastFlow on their own applicative domains. If you interested just write us.
At today, we are developing the following applications:
Micro-benchmarks & Testing Units
They primarily focus to test (in insulation) features and performances of specific Fastflow features. Many of them are written in tutorial style and can be effectively used as fastflow HOWTO (also exploiting the primary computer engineering reusing technique, i.e copy&paste). You can find these apps under the tests directory, along with makefiles.
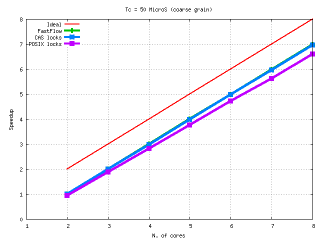
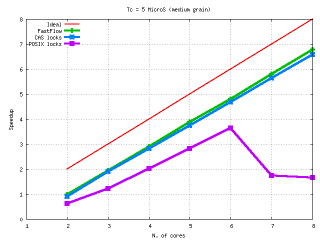
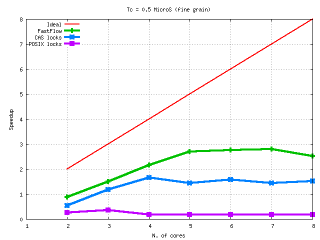
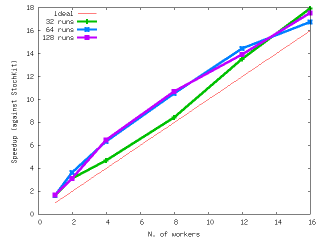
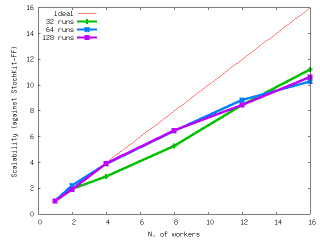
Performances: FastFlow vs POSIX locks and CAS locks
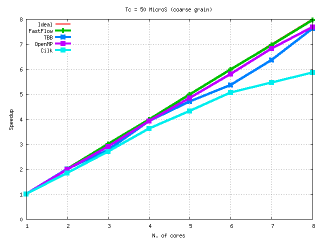
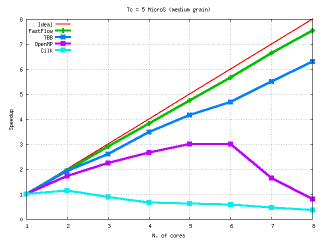
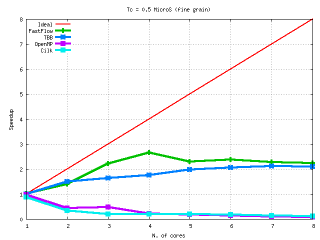
Performances: FastFlow vs Intel TBB vs OpenMP vs Cilk
N-Queens
The N-queens problem is a generalization of the well-known 8-queens problem. N-queens have to be placed on an NxN board-size chess such that no queen can attach the others. The objective is to count all possible solutions.
N-queens problem can be solved recursively (Divide&Conquer) or iteratively. One of the fastest sequential implementations of N-queens is due to Jeff Somers. Somer's N-queens is iterative and written in a heavily optimized C code.
N-queens-Fastflow aims at demonstrating the ability of FastFlow to support the parallelization of heavily optimized legacy codes according with several different methodologies, as for example the “full parallelization” and offloading on FastFlow accelerator.
You can find both the original N-queens and N-queens-FastFlow versions under the applications/nqueens directory, along with makefiles.
Performances
Tests on ottavinareale (8-cores, Linux) using 8 threads.
Tests on dual-quad core Xeon E5520 (8-cores 16-contexts) using 16 threads.
Simple Mandelbrot
Simple Mandelbrot computes and displays the Mandelbrot set. The application has been thought as a naive example of an embarrassingly parallel application on a stream. The mandebrot set is represented as a matrix of pixels. The coordinates of the lines of the complex plane are dispatched by a scheduler thread, which “create a stream” and send its items (lines) to workers in a round robin fashion. Workers allocate a raw of pixels, computes the Mandelbrot set for line and then send the raw of pixel to a collector, which gather the lines from all workers and display them on the screen.
The application has been realised in different version: sequential (mandel_seq), pthread-based (mandel_pt), using fastflow (mandel_ff), using fastflow with FastFlow's memory allocator (mandel_ff_mem_all). All applications use the same sequential code, which has been manually copy&pasted.
Performances are very dependent on the graphic subsystem. So if you want to test performance, please compile all versions with MANDEL_NO_DISPLAY environment variable set (see Makefile). In our tests, the lesser the number of iterations, the higher the FastFlow performance is with respect to the mandel_pt version.
Nokia's QT Mandelbrot
The Trolltech's QT Mandelbrot is an interactive application that computes the Mandelbrot set.
It is part of the Trolltech QT examples and it consists of two
classes: one worker thread that renders the
Mandelbrot set, and another QWidget class that shows the Mandelbrot set on screen and lets the user zoom and scroll. During the time where the worker thread is
recomputing the fractal to reflect the new zoom factor position, the
main thread simply scales the previously rendered pixmap to provide
immediate feedback. The result does not look as good as what the worker
thread eventually ends up providing, but at least it makes the
application more responsive.
These two instances of the classes are run as QT threads; it shows how to use a worker thread to perform heavy computations without blocking the main thread's event loop. The application is multithreaded (exploiting QT threads) but threads are not used to boost heavy computations since the whole computation is done within a single thread, but to decouple two or more activities and to enhance responsiveness. This usage of threads is quite common in real life applications that exploits synchronous network I/O and database access, where the user interface must remain responsive while some heavy operation is taking place.
Despite it an easy application, the full-fledged parallelization of
the whole application is not trivial. The two threads synchronise one
each other via QT events; to guarantee responsiveness the widget thread may start, restart, and abort the activity of worker thread. This kind of behavior, as well as the
integration with other threading libraries, makes non trivial the
porting to frameworks such as TBB and OpenMP. The Fastflow accelerated version just make parallel the worker thread by using a farm FastFlow accelerator.
The original QT Mandelbrot is a multithread application. However, it uses threads just to decouple the graphical widget from Mandelbrot set computation, i.e. to enhance responsiveness not computing time. The FastFlow version achieve both via the semi-automatic parallelization of the workers thread. Notice that, despite multithreaded, the original version cannot be scaled up to more threads because of its design.
This application aims at demonstrating the ability of FastFlow accelerator to support rapid and efficient acceleration, via semi-automatic parallelization of loops, legacy codes exploiting third-party threading models, event structures and callbacks.
You can find three versions (original, with FastFlow accelerator, and with FastFlow acceleraotr and memory allocator) of QT Mandelbrot under the applications/qt-mandelbrot directory, along with the qmake makefiles. Nokia QT 4.x is required to compile and run.
Performances
Tests on magnana (2-cores, Mac OS X 10.6.2 QT 4.6.1).
Smith-Waterman
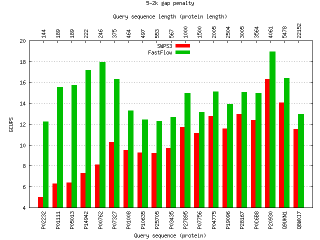
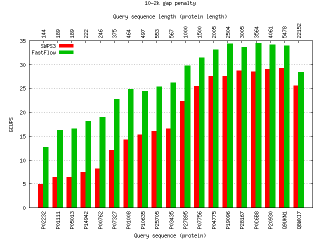
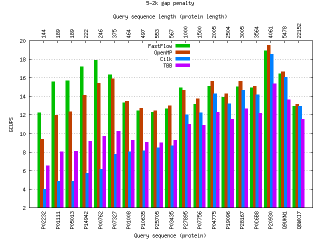
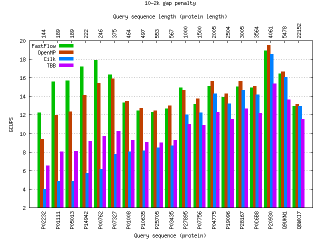
In bioinformatics, sequence database searches are used to find the similarity between a query sequence and subject sequences in the database, in order to discover similar regions between two nucleotide or protein sequences, encoded as a string of characters in an alphabet (e.g. {A,C,G,T}). The sequence similarities can be determined by computing their optimal local alignments using the Smith-Waterman (SW) algorithm. SW is a dynamic programming algorithm that is guaranteed to find the optimal local alignment with respect to the scoring system being used. Instead of looking at the total sequence, the SW algorithm compares segments of all possible lengths and optimises the similarity measure. The cost of this approach is fairly expensive in terms of memory space and computing time (O(mn), where n and m are the lengths of the two sequences), which is increasingly significant with the rapid growth of biological sequence databases.
Smith-Waterman is a well-known CPU-demanding algorithm, because of that is often substituted with other faster but approximated algorithms. Also, its parallelization is fairly challenging because of the very low computation-to-communication ratio exhibited by the analysis of some sequences.
Recent works in this area focus on the implementation of the SW algorithm on many-core architectures like GPUs, Cell/BE and on multi-core architectures exploiting the x86/SSE3 instruction set. From them we selected the SWPS3, which has been extensively optimised to run on Cell/BE and on x86/64 CPUs with SSE3 instructions. The original SWPS3 version is designed as a master-worker computation where the master process distributes the workload to a set of worker processes. The master process handles file I/O and communicates with the worker processes over bidirectional pipes to supply them with database sequences and to collect alignment scores. Every worker computes the alignment of the query sequence with a separate database sequence. We modified the original code to turn it into a FastFlow application by simply (almost syntactically) substituting processes with threads and pipes with FastFlow queues. The master thread (emitter) reads the sequence database and produces a stream of pairs: <query sequence, subject sequence>. The query sequence remains the same for all the subject sequences contained in the database. The worker threads compute the Smith-Waterman algorithm on the input pairs using the SSE3 instructions set. The collector thread gets the resulting score and produces the output string (score and sequence name).
You can find both the original SWPS3 and SWPS3-FastFlow versions under the applications/swps3 directory, along with makefiles.
Performances: FastFlow vs POSIX locks and CAS locks
Performances: FastFlow vs Intel TBB vs OpenMP vs Cilk
FP-growth
Developed together in cooperation with Salvatore Ruggieri, University of Pisa. Development ongoing. Stay tuned.
Cholesky decomposition
The Cholesky decomposition is a decomposition of a symmetric, positive-definite matrix into the product of a lower triangular matrix and its conjugate transpose. Cholesky decomposition could be computed according to several algorithms exploiting different matrix access patterns, which translate in different memory access patterns. Here two versions are compared: the classic algorithm and the block algorithm. The first is computationally lighter but explores the matrixes both by raws and columns …
You can find two Fastflow versions under the applications/cholesky directory, along with makefiles.
pbzip2
PBZIP2 is a parallel implementation by Jeff Gilchrist, of the bzip2 block-sorting file compressor that uses pthreads and achieves near-linear speedup on SMP machines.
We ported the PBZIP2 code under the FastFlow framework; the source code of the new version can be found in pbzip2_ff.cpp. Our main objective in rewriting the application, were to show how to rewrite a pthread-based task-farm application using FastFlow's task-farm schema. A detailed description of the PBZIP2 algorithm can be found in the paper: "Parallel Data Compression with BZIP2" by Jeff Gilchrist
Observe, the main focus of the FastFlow porting is not improving the performance of Gilchrist's PBZIP2, which is already very efficient; it exhibits nearly optimal speedup. The FastFlow porting rather aims to demonstrate that:
- FastFlow makes it possible to achieve the parallelisation of the problem exploiting high-level parallel patterns instead of a hand-tuned design with almost no performance penalty and productivity gain.
- Fastflow non-blocking synchronizations exibit reasonable performances against traditional blocking synchronizations also in worst case scenarios, such as coarse grain elaborations.
In this latter respect, imagine a farm schema where you need the collector filter in order to perform some post elaboration (i.e. writing data into files, buffering tasks for maintaining data ordering, etc.). In this case, the non-blocking collector thread might not have anything to compute for long periods of time because worker threads are slow in producing output tasks. So, it would be better to stop the collector thread letting it wait to be awoken by one of the workers as soon as there are some tasks to post-elaborate. In these situations, non-blocking behaviour might waste CPU cycles, preventing other threads to do something useful (obviously this could happen mainly in those cases where one have more threads than cores).
We proved that by carefully using FastFlow mechanisms you can obtain almost the same linear speedup of the hand-tuned mutex-based version of the same code even in the non optimal case of farm schema with collector filter and coarse grained computation.
Performances
Tests on Andromeda (8-cores 16-Contexts, Linux). bzip2 v.1.0.3, pbzip2 v.1.0.5
| bzip2 (s) | pbzip2 (s) | pbzip2_ff (s) | |
|---|---|---|---|
| Compression | 64.25 | 7.083 | 7.064 |
| Decompression | 14.67 | 1.8260 | 1.8728 |
StochKit-FF
StochKit is an efficient, extensible stochastic simulation framework developed in the C++ language. It implements the popular Gillespie algorithm, explicit and implicit tau-leaping, and trapezoidal tau-leaping methods.
StochKit-FF extends StochKit (v1) with two main features: The support for the parallel run of multiple simulations on multicores, and the support for the online (parallel) reduction of simulation results, which can be performed according to one or more user-defined associative and commutative functions.
StochKit v1 is coded as a sequential C++ application exhibiting several non-reentrant functions, including the random number generation. For this, StochKit-FF represents a significative testbed for the FastFlow ability to support parallelisation of existing complex codes. The parallelisation is supported by means of high-level parallel patterns, which could be also exploited as parametric code factories to parallelise existing, possibly complex C/C++ codes.
StochKit-FF exploits of the FastFlow farm pattern, which implement the functional replication paradigm: a stream of independent data items are dispatched by an Emitter thread to a set of independent Worker threads. Each worker produces a stream of results that is gathered by a Collector thread into a single output stream. Overall, the parallel reduction happens in a systolic (tree) fashion via the so-called selective memory data structure.
Forthcoming. Alpha-developemnt stage. The porting of StochKit on FastFlow is basically a human productivity testbed.
Performances
Tests on ness.epcc.ed.ac.uk (16-cores, Linux).
Two-phase Edge-preserving Denoiser
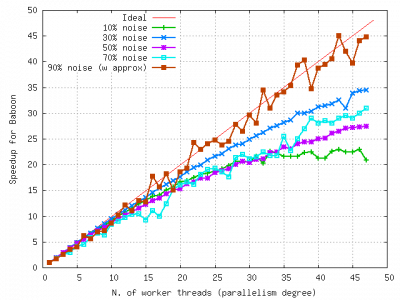
Two-phase Edge-preserving Denoiser is novel FastFlow-based two-step filter for removing salt-and-pepper noise. In the first step, an adaptive median filter is used to identify the set of the noisy pixels; in the second step, these pixels are restored according to a regularization method, which contains a data-fidelity term reflecting the impulse noise characteristics. The application, which exhibits good performance both in denoising and in restoration, can be easily but effectively parallelized to exploit the full power of multi-core CPUs via task offloading; the proposed implementation based on the FastFlow library achieves both close-to-ideal speedup and very good wall-clock execution figures on a common cache-coherent platform such as Intel/AMD multi-core platforms.
The application guarantees a state-of-the-art performance in terms of restoration quality and execution time. Exploiting only a single core it provides the same PSNR/MAE and less than half of the execution time with respect to next best method in literature. In addition, it can benefit from FastFlow acceleration achieving a close to perfect speedup with respect to single core execution.
The code is not of public domain (yet). Please contact us directly if you are interested. This work has been conducted in cooperation with Concetto Spampinato from University of Catania, Italy.
Performances
Example of restoration for Baboon 256×256 standard test with random noise.
| Original | 50% of noise | 70% of noise | 90% of noise |
|---|---|---|---|
 |  |  |  |
| Original | 50% of noise - Restored | 70% of noise - Restored | 90% of noise - Restored |
 |  |  |  |
Restoration quality metrics
| Restoration quality 256×256 | 10% | 30% | 50% | 70% | 90% |
|---|---|---|---|---|---|
| Peak Signal-Noise Ratio | 35.43 | 29.72 | 26.88 | 24.63 | 21.49 |
| Mean Absolute Error | 0.92 | 3.14 | 5.64 | 8.73 | 15.06 |
Execution time and speedup on AMD Magny-Cours Opteron 6174 @2.2GHz, twelve-cores x 4 CPUs.
| Restoration time (S) | 10% | 30% | 50% | 70% | 90% |
|---|---|---|---|---|---|
| Sequential | 9.30 | 32.92 | 85.34 | 120.58 | 180.04 |
| 12 cores | 0.85 | 2.94 | 8.36 | 12.40 | 14.80 |
| 24 cores | 0.51 | 1.57 | 4.90 | 6.34 | 7.50 |
| 36 cores | 0.42 | 1.19 | 3.70 | 5.32 | 5.20 |
| 48 cores | 0.40 | 0.95 | 3.10 | 3.88 | 4.03 |