FastFlow

The FastFlow tutorial can be dowloaded here (version August 2014). The simple tests and examples contained in the tutorial are available as tgz tarball here.

The FastFlow programming model is a structured parallel programming model. The framework provides several pre defined, general purpose, customizable and composable parallel patterns (or algorithmic skeletons). Any applications whose parallel structure may be modelled using the provided parallel patterns, used alone or in composition, may be implemented using FastFlow.

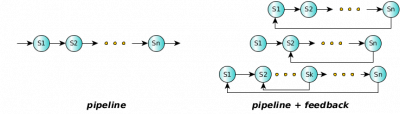
Pipelining is one of the simplest parallel pattern where data flows through a series of stages (or nodes) and each stage processes the input data in some way producing as output a modified version or new data. We will call the data flows streams of data or simply streams. A pipeline's stages can operate sequentially or in parallel and may have or not have an internal state.

/* this is a 3-stage pipeline example */
#include <ff/pipeline.hpp>
using namespace ff;
typedef long fftask_t;
 
struct firstStage: ff_node_t<task_t> {
    fftask_t *svc(fftask_t *t) {
	for(long i=0;i<10;++i) ff_send_out(new fftask_t(i));
	return EOS; // End-Of-Stream
    }
};
fftask_t* secondStage(fftask_t *t,ff_node*const node) {
    std::cout << "Hello I'm stage" << node->get_my_id() << "\n";
    return t;
}
struct thirdStage: ff_node_t<task_t> {
    fftask_t *svc(fftask_t *t) {
	std::cout << "stage" << get_my_id() << " received " << *t << "\n";
        delete t;
	return GO_ON;
    }
};
int main() {
    ff_pipe<fftask_t> pipe(new firstStage, secondStage, new thirdStage);
    pipe.cleanup_nodes(); // cleanup at exit
    if (pipe.run_and_wait_end()<0) error("running pipe");
    return 0;
}

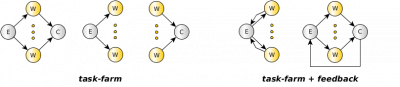
The task-farm pattern is a stream parallel paradigm based on the replication of a purely functional computation (let's call the function F). Its parallel semantics ensures that it will process tasks such that the single task latency is close to the time needed to compute the function F sequentially, while the throughput (under certain conditions) is close to F/n where n is the number of parallel agents used to execute the farm (called Workers). The concurrent scheme of a farm is composed of three distinct parts: the Emitter (E), the pool of workers (Ws) and the Collector (C). The emitter gets farm's input tasks and distributes them to workers using a given scheduling strategy (round-robin, auto-scheduling, user-defined). The collector collects tasks from workers and sends them to the farm's output stream.

/* the third stage is transformed in a farm */
#include <ff/farm.hpp>
#include <ff/pipeline.hpp>
...
 
int main() {
    std::vector<ff_node*> W = {new thirdStage, new thirdStage}; // the farm has 2 workers
    ff_pipe<fftask_t> pipe(new firstStage, secondStage, new ff_farm<>(W));
    pipe.cleanup_nodes();
    if (pipe.run_and_wait_end()<0) error("running pipe");
    return 0;
}

A sequential iterative kernel with independent iterations is also known as a par- allel loop. Parallel loops may be clearly parallelized by using the map or farm patterns, but this typically requires a substantial re-factoring of the original loop code with the possibility to introduce bugs and not preserving sequential equivalence. In the FastFlow framework there are a set of data parallel patterns implemented on top of the basic FastFlow skeletons to ease the implementation of parallel loops: ParallelFor, ParallelForReduce, ParallelForPipeReduce.

Heare a very basic usage example of the ParallelFor pattern:

#include <ff/parallel_for.hpp>
using namespace ff;
int main() {
    long A[100];
    ParallelFor pf;
    pf.parallel_for(0,100,[&A](const long i) {
      A[i] = i;
    });
    ...
    return 0;
}

Summary

Chapter 1
Introduction

FastFlow is an open-source, structured parallel programming framework originally conceived to support highly efficient stream parallel computation while targeting shared memory multi-core. Its efficiency comes mainly from the optimised implementation of the base communication mechanisms and from its layered design. FastFlow provides the parallel applications programmer with a set of ready-to-use, parametric algorithmic skeletons modelling the most common parallelism exploitation patterns. The algorithmic skeletons provided by FastFlow may be freely nested to model more and more complex parallelism exploitation patterns.

FastFlow is an algorithmic skeleton programming framework developed and maintained by the parallel computing group at the Departments of Computer Science of the Universities of Pisa and Torino [9].

---

---

Fig. 1.1 presents a brief history of the algorithmic skeleton programming model. For a more in-depth description, please refer to [14].

A number of papers and technical reports discuss the different features of this programming environment [10, 5, 2], the results achieved when parallelizing different applications [18, 11, 15, 8, 1, 7, 6] and the use of FastFlow as software accelerator, i.e. as a mechanism suitable for exploiting unused cores of a multi-core architecture to speed up execution of sequential code [3, 4]. This work represents instead a tutorial aimed at describing the use of the main FastFlow skeletons and patterns and its programming techniques, providing a number of simple (and not so simple) usage examples.

This tutorial describes the basic FastFlow concepts and the main skeletons targeting stream-parallelism, data-parallelism and data-flow parallelism. It is still not fully complete: for example important arguments and FastFlow features such as the FastFlow memory allocator, the thread to core affinity mapping, GPGPU programming and distributed systems programming are not yet covered in this tutorial.

This tutorial is organised as follow: Sec. 1.1 describes how to download the framework and compile programs, Sec. 2 recalls the FastFlow application design principles. Then, in Sec. 3 we introduce the main features of the stream-based parallel programming in FastFlow: how to wrap sequential code for handling a steam of data, how to generate streams and how to combine pipelines, farms and loop skeletons, how to set up farms and pipelines as software accelerator. In Sec. 4 we introduce data-parallel computations in FastFlow. ParallelFor, ParallelForReduce, ParallelForPipeReduce and Map are presented in this section. Finally, in Sec. 5, the macro data-flow programming model provided by the FastFlow framework is presented.

1.1 Installation and program compilation

FastFlow is provided as a set of header files. Therefore the installation process is trivial, as it only requires to download the last version of the FastFlow source code from the SourceForge (http://sourceforge.net/projects/mc-fastflow/) by using svn:

Once the code has been downloaded (with the above svn command, a fastflow folder will be created in the current directory), the directory containing the ff sub-directory with the FastFlow header files should be named in the -I flag of g++, such that the header files may be correctly found.

For convenience may be useful to set the environment variable FF_ROOT to point to the FastFlow source directory. For example, if the FastFlow tarball (or the svn checkout) is extracted into your home directory with the name fastflow, you may set FF_ROOT as follows (bash syntax):

Take into account that, since FastFlow is provided as a set of .hpp source files, the -O3 switch is essential to obtain good performance. Compiling with no -O3 compiler flag will lead to poor performance because the run-time code will not be optimised by the compiler. Also, remember that the correct compilation of FastFlow programs requires linking the pthread library (-lpthread flag).

1.1.1 Tests and examples

In this tutorial a set of simple usage examples and small applications are described. In almost all cases, the code can be directly copy-pasted into a text editor and then compiled as described above. For convenience all codes are provided in a separate tarball file fftutorial_source_code.tgz with a Makefile.

At the beginning of all tests and examples presented, there is included the file name containing the code ready to be compiled and executed, for example:

means that the above code is in the file hello_node.cpp.

Chapter 2
Design principles

FastFlow has been originally designed to provide programmers with efficient parallelism exploitation patterns suitable to implement (fine grain) stream parallel applications. In particular, FastFlow has been designed

• to promote high-level parallel programming, and in particular skeletal programming (i.e. pattern-based explicit parallel programming), and
• to promote efficient programming of applications for multi-core.

More recently, within the activities of the EU FP7 STREP project ”ParaPhrase”¹ the FastFlow framework has been extended in several ways. In particular, in the framework have been added:

• several new high-level patterns
• facilities to support coordinated execution of FastFlow program on distributed multi-core machines
• support for execution of new data parallel patterns on GPGPUs
• new low-level parallel building blocks allowing to build almost any kind of streaming graph and parallel patterns.

The whole programming framework has been incrementally developed according to a layered design on top of Pthread/C++ standard programming framework as sketched in Fig. 2.1).

---

---

The Building blocks layer provides the basics blocks to build (and generate via C++ header-only templates) the run-time support of core patterns. Typical objects at this level are queues (e.g. lock-free SPSC queues, bounded and unbounded), process and thread containers (as C++ classes) mediator threads/processes (extensible and configurable schedulers and gatherers). The shared-memory run-time support extensively uses non-blocking lock-free algorithms, the distributed run-time support employs zero-copy messaging, the GPGPUs support exploits asynchrony and SIMT optimised algorithms.

The Core patterns layer provides a general data-centric parallel programming model with its run-time support, which is designed to be minimal and reduce to the minimum typical sources of overheads in parallel programming. At this level there are two patterns (task-farm and all its variants and pipeline) and one pattern-modifier (feedback). They make it possible to build very general (deadlock-free) cyclic process networks. They are not graphs of tasks, they are graphs of parallel executors (processes/threads). Tasks or data items flows across them according to the data-flow model. Overall, the programming model can be envisioned as a shared-memory streaming model, i.e. a shared-memory model equipped with message-passing synchronisations. They are implemented on top of building blocks.

The High-level patterns are clearly characterised in a specific usage context and are targeted to the parallelisation of sequential (legacy) code. Examples are exploitation of loop parallelism (ParallelFor and its variants), stream parallelism (pipeline and task-farm), data-parallel algorithms (map, poolEvolution, stencil, StencilReduce), execution of general workflows of tasks (mdf - Macro Data-Flow), etc. They are typically equipped with self-optimisation capabilities (e.g. load-balancing, grain auto-tuning, parallelism-degree auto-tuning) and exhibit limited nesting capability. Some of them targets specific devices (e.g. GPGPUs). They are implemented on top of core patterns.

Parallel application programmers are supposed to use FastFlow directly exploiting the parallel patterns available at the ”High-level” or ”Core” levels. In particular:

• defining sequential concurrent activities, by sub classing a proper FastFlow class, the ff_node (or ff_minode and ff_monode) class, and
• building complex stream parallel patterns by hierarchically composing sequential concurrent activities, pipeline patterns, feedbacks, task-farm patterns and their ”specialised” versions implementing more complex parallel patterns.

Concerning the usage of FastFlow to support parallel application development on shared memory multi-core, the framework provides two possible abstractions of structured parallel computation:

• a skeleton program abstraction used to implement applications completely modelled according to the algorithmic skeleton concepts. When using this abstraction, the programmer writes a parallel application by providing the business logic code, wrapped into proper ff_node sub-classes, a skeleton (composition) modelling the parallelism exploitation pattern of the application and a single command starting the skeleton computation and awaiting for its termination.
• an accelerator abstraction used to parallelize (and therefore to accelerate) only some parts of an existing application. In this case, the programmer provides a skeleton composition which is run on the ”spare” cores of the architecture and implements a parallel version of part of the business logic of the application, e.g. the one computing a given f(x). The skeleton composition, if operating on stream (i.e. pipeline or task-farm based compositions), will have its own input and output channels. When an f(x_j) has to be computed within the application, rather than writing code to call to the sequential f code, the programmer may insert asynchronous ”offloading” calls for sending x_j to the accelerator skeleton. Later on, when the result of f(x_j) has to be used, the code needed for ”reading” accelerator results may be used to retrieve the computed values.

This second abstraction fully implements the ”minimal disruption” principle stated by Cole in his skeleton manifesto [13], as the programmer using the accelerator is only required to program a couple of offload/get_result primitives in place of the single … = f(x) function call statement (see Sec. 3.7).

Chapter 3
Stream parallelism

An application may operate on values organised as streams. A stream is a possibly infinite sequence of values, all of them having the same data type, e.g. a stream of images (not necessarily all having the same format), a stream of files, a stream of network packets, a stream of bits, etc.

A complex streaming application may be seen as a graph (or workflow) of computing modules (sequential or parallels) whose arcs connecting them bring streams of data of different types. The typical requirements of such a complex streaming application is to guarantee a given Quality of Service imposed by the application context. In a nutshell, that means that the modules of the workflow describing the application have to be able to sustain a given throughput.

There are many applications in which the input streams are primitive, because they are generated by external sources (e.g. HW sensors, networks, etc..) or I/O. However, there are cases in which streams are not primitive, but it is possible that they can be generated directly within the program. For example, sequential loops or iterators. In the following we will see how to generate a stream of data in FastFlow starting from sequential loops.

3.1 Stream parallel skeletons

Stream parallel skeletons are those natively operating on streams, notably pipeline and task-farm (or simply farm).

pipeline

The pipeline skeleton is typically used to model computations expressed in stages. In the general case, a pipeline may have more than two stages, and it can be built as a single pipeline with N stages or as pipeline of pipelines. Given a stream of input tasks

the pipeline with stages

computes the output stream

The parallel semantics of the pipeline skeleton ensures that all the stages will be execute in parallel. It is possible to demonstrate that the total time required to entirely compute a single task (latency) is close to the sum of the times required to compute the different stages. And, the time needed to output a new result (throughput) is close to time spent to compute a single task by the slowest stage in the pipeline.

task-farm

The task-farm (sometimes also called master-worker) is a stream parallel paradigm based on the replication of a purely functional computation. The farm skeleton is used to model embarrassingly parallel computations. The only functional parameter of a farm is the function f needed to compute the single task. The function f is stateless. Only under particular conditions, functions with internal state, may be used.

Given a stream of input tasks

the farm with function f computes the output stream

Its parallel semantics ensures that it will process tasks such that the single task latency is close to the time needed to compute the function f sequentially, while the throughput (only under certain conditions) is close to where n is the number of parallel agents used to execute the farm (called workers), i.e. its parallelism degree.

The concurrent scheme of a farm is composed of three distinct parts: the Emitter, the pool of workers and the Collector. The Emitter gets a farm’s input tasks and distributes them to workers using a given scheduling strategy. The Collector collects tasks from workers and sends them to the farm’s output stream.

---

---

3.2 FastFlow abstractions

In this section we describe the sequential concurrent activities (ff_node, ff_minode, ff_monode and ff_dnode), and the ”core” skeletons pipeline and task-farm (see Fig 3.1) used as building blocks to model composition and parallel executions. The core skeletons are ff_node derived objects as well, so they can be nested and composed in almost any arbitrary way. The feedback pattern modifier can also be used in the pipeline and task-farm to build complex cyclic streaming networks.

3.2.1 ff_node

The ff_node sequential concurrent activity abstraction provides a means to define a sequential activity (via its svc method) that a) processes data items appearing on a single input channel and b) delivers the related results onto a single output channel.

In a multi-core, a ff_node object is implemented as a non-blocking thread (or a set of non-blocking threads). This means that the number of ff_node(s) concurrently running should not exceed the number of logical cores of the platform at hand.

The ff_node class actually defines a number of methods, the following three virtual methods are of particular importance:

The first is the one defining the behaviour of the node while processing the input stream data items. The other two methods are automatically invoked once and for all by the FastFlow RTS when the concurrent activity represented by the node is started (svc_init) and right before it is terminated (svc_end). These virtual methods may be overwritten in the user supplied ff_node sub-classes to implement initialisation code and finalisation code, respectively. Since the svc method is a pure virtual function, it must be overwritten.

A FastFlow ff_node can be defined as follow:

The ff_node behaves as a loop that gets an input task (coming from the input channel), i.e. the input parameter of the svc method, and produces one or more outputs, i.e. the return value of the svc method or the invocation of the ff_send_out method that can be called inside the svc method. The loop terminates either if the output provided or the input received is a special value: ”End-Of-Stream” (EOS). The EOS is propagated across channels to the next ff_node.

Particular cases of ff_nodes may be simply implemented with no input channel or no output channel. The former is used to install a concurrent activity generating an output stream (e.g. from data items read from keyboard or from a disk file); the latter to install a concurrent activity consuming an input stream (e.g. to present results on a video, to store them on disk or to send output packets into the network).

The simplified life cycle of an ff_node is informally described in the following pseudo-code:

It is also possible to return from a ff_node the value GO_ON. This special value tells the run-time system (RTS) that there are no more tasks to send to the next stage and that the ff_node is ready to receive the next input task (if any). The GO_ON task is not propagated to the next stage. Other special values can be returned by an ff_node, such as GO_OUT and EOS_NOFREEZE, both of which are not propagated to the next stages and are used to exit the main node loop. The difference is that while GO_OUT allows the thread to be put to sleep (if it has been started with run_then_freeze), the second one instead allows to jump directly to the point where input channels are checked for receiving new tasks without having the possibility to stop the thread.

An ff_node cannot be started alone (unless the method run() and wait() are overwritten). Instead, it is assumed that ff_node derived objects are used as pipeline stages or task-farm workers. In order to show how to execute and wait for termination of ff_node derived objects, we provide here a simple wrapper class (in the next sections we will see that pipeline and task-farm are ff_node derived objects) :

In this example, a myNode has been defined redefining all methods needed to execute the node, put the node to sleep (freeze the node), wake-up the node (thaw the node) and waiting for its termination.

Line 41 starts the computation of the node and waits for its termination synchronously. At line 46 the node is started again but in this case the run_then_freeze method first sets the ff_node::freezing flag and then starts the node (i.e. creates the thread which execute the node). The ff_node::freezing flag tells the run-time that the node has to be put to sleep (frozen using our terminology) instead of terminating it when an EOS is received in input or it is returned by the node itself. The node runs asynchronously with respect to the main thread, so in order to synchronise the executions, the wait_freezing method is used (it waits until the node is frozen by the FastFlow run-time). When the run_then_freeze method is called again, since the node is frozen, instead of starting another thread, the run-time just ”thaws” the thread.

---

---

3.2.2 ff_pipe

Pipeline skeletons in FastFlow can be easily instantiated using the C++11-based constructors available in the latest release of FastFlow.

The standard way to create a pipeline of n different stages in FastFlow is to create n distinct ff_node objects and then pass them in the correct order to the ff_pipe constructor¹ . For example, the following code creates a 3-stage pipeline:

To execute the pipeline it is possible to use the run_and_wait_end() method. This method starts the pipeline and synchronously waits for its termination ².

For example, the following

The ff_pipe constructor also accepts as pipeline stage functions with signature T⋆(⋆F)(T⋆,ff_node⋆const). This is because in many situations it is simpler to write a function than an ff_node. The FastFlow run-time wraps those functions in a ff_node object whose pointer is passed as second parameter to the function.

As an example consider the following 3-stage pipeline :

Here 2 functions getting a myTask pointer as input and return type are used as first and third stage of the pipeline whereas an ff_node object is used for the middle stage. Note that the first stage, generates 10 tasks and then an EOS.

Finally, it is also possible to add stages (of type ff_node) to a pipeline using the add_stage method as in the following sketch of code:

3.2.3 ff_minode and ff_monode

The ff_minode and the ff_monode are multi-input and multi-output FastFlow nodes, respectively. By using these kinds of node, it is possible to build more complex skeleton structures. For example, the following code implements a 4-stage pipeline where each stage sends some of the tasks received in input back to the first stage.

To create a loopback channel we have used the wrap_around method available in both the ff_pipe and the ff_farm skeletons. More details on feedback channels in Sec. 3.5.

---

---

3.2.4 ff_farm

Here we introduce the other primitive skeleton provided in FastFlow, namely the ff_farm skeleton.

The standard way to create a task-farm skeleton with n workers is to create n distinct ff_node objects (workers node), pack them in a std::vector and then pass the vector to the ff_farm constructor. Let’s have a look at the following ”hello world”-like program:

This code basically defines a farm with nworkers workers processing data items appearing onto the farm input stream and delivering results onto the farm output stream. The default scheduling policy used to send input tasks to workers is the ”pseudo round-robin one” (see Sec. 3.3). Workers are implemented by the Worker objects. These objects may represent sequential concurrent activities as well as further skeletons, that is either pipeline or farm instances. The above defined farm myFarm has the default Emitter (or scheduler) and the default Collector (or gatherer) implemented as separate concurrent activity. To execute the farm synchronously, the run_and_wait_end() method is used.

Compiling and running the above code we have:

As you can see, the workers are activated only once because there is no input stream. The only way to provide an input stream to a FastFlow streaming network is to have the first component in the network generating a stream or by reading a ”real” input stream. To this end, we may for example use the farm described above as a second stage of a pipeline skeleton whose first stage generates the stream and the last stage just writes the results on the screen:

In some cases, could be convinient to create a task-farm just from a single function (i.e. withouth defining the ff_node). Provided that the function has a proper signature, i.e. T⋆(⋆F)(T⋆,ff_node⋆const), a very simple way to instanciate a farm is to pass the function and the number of workers you want to use (replication degree) in the ff_farm construct, as in the following sketch of code:

Defining Emitter and Collector in a farm

Both emitter and collector must be supplied as ff_node to the farm constructor. Considering the farm skeleton as a particular case of a a 3-stage pipeline (the first stage and the last stage are the Emitter and the Collector, respectively) we now want to re-write the previous example using only the FastFlow farm skeleton:

The Emitter node encapsulates user’s code provided in the svc method and the task scheduling policy which defines how tasks will be sent to workers. In the same way, the Collector node encapsulates the user’s code and the task gathering policy defining how tasks have to be collected from the workers.

It is possible to redefine both scheduling and gathering policies of the FastFlow farm skeleton, please refer to to [16].

Farm with no Collector

We consider now a further case: a farm with the Emitter but without the Collector. Having no collector the farm’s workers may either consolidates the results in the main memory or send them to the next stage (in case the farm is a pipeline stage) provided that the next stage is defined as ff_minode (i.e. multi-input node).

It is possible to remove the collector from the ff_farm by calling the method remove_collector. Let’s see a simple example implementing the above case:

3.3 Tasks scheduling

Sending tasks to specific farm workers

In order to select the worker where an incoming input task has to be directed, the FastFlow farm uses an internal ff_loadbalancer that provides a method int selectworker() returning the index in the worker array corresponding to the worker where the next task has to be directed. The programmer may subclass the ff_loadbalancer and provide his own selectworker() method and then pass the new load balancer to the farm emitter, therefore implementing a farm with a user defined scheduling policy. To understand how to do this, please refer to [16].

Another simpler option for scheduling tasks directly in the svc method of the farm emitter is to use the ff_send_out_to method of the ff_loadbalancer class. In this case what is needed is to pass the default load balancer object to the emitter thread and to use the ff_loadbalancer::ff_send_out_to method instead of ff_node::ff_send_out method for sending out tasks.

Let’s see a simple example showing how to send the first and last task to a specific workers (worker 0).

Broadcasting a task to all workers

FastFlow supports the possibility to direct a task to all the workers in the farm. It is particularly useful if we want to process the task by workers implementing different functions (so called MISD farm). The broadcasting is achieved calling the broadcast_task method of the farm ff_loadbalancer object, in a very similar way to what we have already seen for the ff_send_out_to method in the previous section.

In the following a simple example.

Using auto-scheduling

The default farm scheduling policy is ”loosely round-robin” (or pseudo round-robin) meaning that the Emitter try to send the task in a round-robin fashion, but in case one of the workers’ input queue is full, the Emitter does not wait till it can insert the task in the queue, but jumps to the next worker until the task can be inserted in one of the queues. This is a very simple policy but it doesn’t work well if the tasks have very different execution costs.

FastFlow provides a suitable way to define a task-farm skeleton with the ”auto-scheduling” policy. When using such policy, the workers ”ask” for a task to be computed rather than (passively) accepting tasks sent by the emitter (explicit or implicit) according to some scheduling policy. This scheduling behaviour may be simply implemented by using the method set_scheduling_ondemand() of the ff_farm class, as in the following:

It is worth to remark that, this policy is able to ensure quite good load balancing property when the tasks to be computed exhibit different computational costs and up to the point when the Emitter does not become a bottleneck.

It is possible to increase the asynchrony level of the ”request-reply” protocol between workers and Emitter simply by passing an integer value grater than zero to the set_scheduling_ondemand() function. By default the asynchrony level is 1.

3.4 Tasks ordering

Tasks passing through a task-farm can be subjected to reordering because of different execution times in the worker threads. To overcome the problem of sending packets in a different order with respect to input, tasks can be reordered by the Collector. This solution might introduce extra latency mainly because reordering checks have to be executed even in the case packets already arrive at the farm Collector in the correct order.

The default round-robin and auto scheduling policies are not order preserving, for this reason a specialised version of the FastFlow farm has been introduced which enforce the ordering of the packets.

The ordered farm may be introduced by using the ff_ofarm skeleton.
TBD: put an example here

3.5 Feedback channels

There are cases where it is useful to have the possibility to route back some results to the streaming network input stream for further computation. For example, this possibility may be exploited to implement the divide&conquer pattern using the task-farm.

The feedback channel in a farm or pipeline may be introduced by the wrap_around method on the interested skeleton. As an example, in the following code it is implemented a task-farm with default Emitter and Collector and with a feedback channel between the Collector and the Emitter:

Starting with FastFlow version 2.0.0, it is possible to use feedback channels not only at the outermost skeleton level. As an example, in the following we provide the code needed to create a 2-stage pipeline where the second stage is a farm without Collector and a feedback channel between each worker and the farm Emitter:

In this case the Emitter node of the farm receives tasks both from the first stage of the pipeline and from farm’s workers. To discern different inputs it is used the ff_get_channel_id method of the ff_loadbalancer object: inputs coming from workers have channel id greater than 0 (the channel id correspond to the worker id). The Emitter non-deterministic way processes input tasks giving higher priority to the tasks coming back from workers.

It is important to note how EOS propagation works in presence of loopback channels. Normally, the EOS is automatically propagated onward by the FastFlow run-time in order to implement pipeline-like termination. When internal loopback channels are present in the skeleton tree (and in general when there is multi-input nodes), the EOS is propagated only if the EOS message has been received from all input channels. In this case is useful to be notified when an EOS is received so that the termination can be controlled by the programmer. In the proposed example above, we want to propagate the EOS as soon as we receive it from the Stage0 and then to terminate the execution only after having received all EOS from all workers.

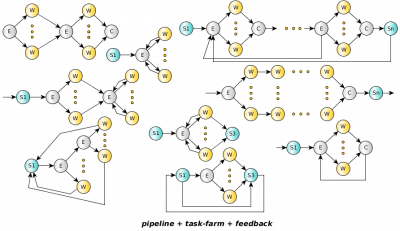
3.6 Mixing farms pipelines and feedbacks

---

---

FastFlow pipeline, task-farm skeletons and the feedback pattern modifier can be nested and combined in many different ways. Figure 3.4 sketches some of the possible combinations that can be realised in a easy way.

3.7 Software accelerators

FastFlow can be used to accelerate existing sequential code without the need of completely restructuring the entire application using algorithmic skeletons. In a nutshell, programmers may identify potentially concurrent tasks within the sequential code and request their execution from an appropriate FastFlow pattern on the fly.

By analogy with what happens with GPGPUs and FPGAs used to support computations on the main processing unit, the cores used to run the user defined tasks through FastFlow define a software ”accelerator” device. This device will run on the ”spare” cores available. FastFlow accelerator is a ”software device” that can be used to speedup portions of code using the cores left unused by the main application. From a more formal perspective, a FastFlow accelerator is defined by a skeletal composition augmented with an input and an output stream that can be, respectively, pushed and popped from outside the accelerator. Both the functional and extra-functional behaviour of the accelerator is fully determined by the chosen skeletal composition.

---

---

Using FastFlow accelerator mode is not that different from using FastFlow to write an application only using skeletons (see Fig. 3.5). The skeletons must be started as a software accelerator, and tasks have to be offloaded from the main program. A simple program using the FastFlow accelerator mode is shown below:

The ”true” parameter in the farm constructor (the same is for the pipeline) is the one telling the run-time that the farm (or pipeline) has to be used as an accelerator. The idea is to start (or re-start) the accelerator and whenever we have a task ready to be submitted to the accelerator, we simply ”offload” it to the accelerator. When we have no more tasks to offload, we send the End-Of-Stream and eventually we wait for the completion of the computation of tasks in the accelerator or, we can wait_freezing to temporary stop the accelerator without terminating the threads in order to restart the accelerator afterwards.

The bool load_result(void ⋆⋆) methods synchronously await for one item being delivered on the accelerator output stream. If such item is available, the method returns ”true” and stores the item pointer in the parameter. If no other items will be available, the method returns ”false”. An asynchronous method is also available with signature bool load\_results\_nb(void ⋆⋆) When the method is called, if no result is available, it returns ”false”, and might retry later on to see whether a result is ready.

3.8 Examples

---

---

In this sections we consider an images filtering application in which 2 image filters have to be applied to a stream of images. We prove different possible FastFlow implementation using both pipeline and task-farm skeletons. The different implementations described in the following are sketched in Fig. 3.6 (all but versions img_farm2.cpp and img_farm3.cpp are reported as source code in this tutorial): the starting sequential implementation (img.cpp), a 4-stage FastFlow pipeline implementation (img_pipe.cpp), the same version as before but the pipeline (3-stage) is implemented as a ”software accelerator” while the image reader stage is directly the main program (img_pipe2.cpp), a 4-stage FastFlow pipeline with the second and third stages implemented as task-farm skeletons (img_pipe+farm.cpp), a variant of the previous case, i.e. a 3-stage pipeline whose middle stage is a farm whose workers are 2-stage pipelines (img_farm+pipe.cpp), and finally the so called ”normal-form”, i.e. a single task-farm having the image reader stage collapsed with the farm Emitter and having the image writer stage collapsed with the farm collector (img_farm.cpp). The last 2 versions (not reported as source code here), i.e. img_farm2.cpp and img_farm3.cpp, are incremental optimizations of the base img_farm.cpp version in which the input and output is performed in parallel in the farm’s workers.

3.8.1 Images filtering

Let’s consider a simple streaming application: two image filters (blur and emboss) have to be applied to a stream of input images. The stream can be of any length and images of any size (and of different format). For the sake of simplicity images’ file are stored in a disk directory and the file names are passed as command line arguments of our simple application. The output images are stored with the same name in a separate directory.

The application uses the ImageMagick library³ to manipulate the images and to apply the two filters. In case the ImageMagick library is not installed, please refer to the ”Install from Source” instructions contained in the project web site. This is our starting sequential program:

Since the two filters may be applied in sequence to independent input images, we can compute the two filters in pipeline. So we define a 4-stage pipeline: the first stage read images from the disk, the second and third stages apply the two filters and the forth stage writes the resulting image into the disk (in a separate directory). The code for implementing the pipeline is in the following:

It is possible to instantiate the pipeline as a software accelerator. In the following we report only the code of the main function since it is the only part of the code that differs:

Now, since the same filter may be applied in parallel to independent input images, we can replace the second and third stage with two task-farm having the same previous stage as worker. This is safe because we know that we can replicate the function computing the filters: it is thread safe and has no internal shared state. The resulting code is:

A possible variant of the previous implementation, which uses only one scheduler is the following one:

The next step is to reduce the number of resources used. For example the farm Emitter can be used to read files from the disk, whereas the farm Collector for writing files to the disk. Furthermore, the blur and emboss filters may be computed sequentially using a single workers. This is the so called ”normal form” obtained optimising the resource usage. The code implementing the normal form is the following:

Chapter 4
Data parallelism

In data parallel computation, data structures (typically large) are partitioned among the number of concurrent resources each of which computes the same function on the assigned partition. In a nutshell, the input task, possibly but not necessarily coming from an input stream, is split into multiple sub-task each one computed in parallel and then collected together in one single output task. The computation on the sub-tasks may be completely independent (i.e. the sub-task computation uses data only coming from the the current sub-task) or dependent on previously computed data (non necessarily in the corresponding sub-task). The main goal of data parallel computation is to reduce the completion time of the single task to compute. It is important to note that, data decomposition using large sub-tasks, together with static assignment of such partitions to workers, may introduce load imbalance during the computation mainly because of the variable calculation time associated to distinct partitions. In general, it is possible to state that load balancing is a feature of anonymous task assignment, i.e. tasks to be computed are dynamically assigned to available computing resources, without a-priori correspondence between tasks and available computing resources. The task-farm paradigm is naturally based on this concept (where tasks are stream items), and for this reason quite often data-parallel computations are implemented on top of the task-farm skeleton by using the auto-scheduling policy (see Sec. 3.3). Many other scheduling strategies have been devised for balancing data-parallel computations, among these, the work-stealing scheduling strategy is of particular importance. It is worth to note here that, when the task-farm is used to implement an unbalanced data parallel computation, it is possible to ”customise” it to use a work-stealing scheduling strategy. In other words, the task-farm pattern just models functional replication, while data partitioning and task-scheduling depends on the way the Emitter entity is implemented.

Well known and widely used data parallel skeletons are: map reduce and stencil.

4.1 Data parallel skeletons

In this section we describe map-like and reduce-like patterns, whereas the stencil pattern is not covered.

map

The simplest data parallel computation is the map, in which the concurrent workers operating on a partition of the input data structure (typically an N-dimensional array) are fully independent, i.e. each of them operates on its own local data only, without any cooperation with other computing resources. As an example consider the following piece of code:

If the function F has no internal state, each loop iteration may be computed independently since there are no true dependency among iterations. In this case we may apply the map pattern, splitting the two arrays A,B in n = parts and assign each part to one worker. Each worker executes the same loop as above on a restricted index range. In principle, the execution time can be reduced by a factor of n if we consider a run-time with zero overhead, and as a particular case, if nworkers = N, the execution time is reduced from O(N) to O(1). It is worth to note that, the map skeleton may be simply implemented using a task-farm skeleton operating on a single input data. The Emitter split the input arrays and distributes the partitions to each worker. The workers apply the function F on the input partition, finally the Collector collects the workers’ partitions in one single output task.

Loop-parallelism

A sequential iterative kernel with independent iterations is also known as a parallel loop. Parallel loops may be clearly parallelized by using the map or farm skeletons, but this typically requires a substantial re-factoring of the original loop code with the possibility to introduce bugs and not preserving sequential equivalence. Furthermore, the selection of the appropriate implementation skeleton together with a correct implementation of the sequential wrapper code is of foremost importance for obtaining the best performance.

For these reasons, in the FastFlow framework there are a set of data parallel patterns implemented on top of the basic FastFlow skeletons to ease the implementation of parallel loops.

4.2 FastFlow abstractions

In this section we describe the different parallel-for abstractions that are used to implement almost all data-parallel skeletons currently available in the FastFlow framework for multi-core systems.

4.2.1 ParallelFor

Here we introduce the FastFlow ParallelFor pattern that can be used to parallelize loops having independent iterations:

The class interface of the ParallelFor pattern is described in the parallel_for.hpp file. The constructor accepts two parameters:

the first parameter sets the maximum number of worker threads that can be used in the ParallelFor (that is the maximum concurrency degree), the second argument sets non-blocking run-time for parallel computations. At the beginning you may just leave the default parameters for these two arguments.

The ParallelFor object, encapsulates a number of parallel_for methods, which differentiate each other for the number of arguments they get and for the signatures of the function body. A single ParallelFor object can be used as many times as needed to run different parallel-for instances (different loop bodies). Nested invocations of ParallelFor methods are not supported.

The loop body may be a standard function or a C++11 lambda-function. A C++11 lambda-function is a new feature of the C++11 standard already supported by many compilers. They are unnamed closures (i.e. function objects that can be constructed and managed like data) that allow functions to be syntactically defined where and when needed. When lambda functions are built, they can capture the state of non-local variables named in the wrapped code either by value or by reference.

The following list presents the most useful parallel-for methods provided by the ParallelFor class:

Now, given the following sequential loop:

we can write the following parallel-for:

or by using the parallel_for_idx we have:

the parallel_for_idx is just a ”low-level” version of the parallel_for, where the internal loop, iterating over all iterations assigned to the worker, has to be written directly by the user. This may be useful when it is needed to execute a pre-computation (executed in parallel) before starting the execution of the loop iterations, or in general for debugging purposes.

It is important to remark that, when spinWait is set to true (see Sec. 4.2.1 for details), in some particular cases, the body function is called the first time with begin==end==0 so it would be safe to test this condition at the beginning of the parallel_for_idx (i.e. if (begin==end) return;).

Let’s now see a very simple usage example of the parallel-for:

in this case, first the array A has been initialised using a parallel-for and then the square value of the even entries is computed in parallel over N∕2 iterations.

Iterations scheduling

Three distinct iteration schedulings are currently possible in parallel-for computations:

1.

default static scheduling: the iteration space is (almost) evenly partitioned in large contiguous chunks, and then they are statically assigned to workers, one chunk for each worker.

2.

static scheduling with interleaving k: the iteration space is statically divided among all active workers in a round-robin fashion using a stride of k. For example, to execute 10 iterations (from 0 to 9) using a concurrency degree of 2 and a stride k = 3, then the first thread executes iterations 0,1,2,6,7,8 and the second thread executes iterations 3,4,5,9. The default static scheduling is obtained setting a stride k = iterationspace∕nworkers.

3.

dynamic scheduling with chunk k: in this case no more than k contiguous iterations at a time are dynamically assigned to computing workers. As soon as a worker completes computation of one chunk of iterations, a new chunk (if available) is selected and assigned to the worker. The run-time tries to select as many as possible contiguous chunks in order to better exploit spatial locality. This allows to have a good trade-off between iterations affinity and load-balancing.

By default the default static scheduling is used. In general, the scheduling policy is selected by specifying the grain parameter of the parallel_for method. If the grain parameter is not specified or if its value is 0, then the default static scheduling is selected. If grain is greater than zero, then the dynamic scheduling is selected with k = grain. Finally, to use the static scheduling with interleaving k the parallel_for_static method must be used with k = grain. Note that, if in the parallel_for_static the grain parameter is zero, than the default static scheduling policy is selected.

Summarising, in the following different scheduling strategies are selected according to the grain parameter:

threadPause and disableScheduler

The spinWait parameter in the ParallelFor constructor enables non-blocking computation between successive calls of parallel_for methods. This means that if the parallel-for is not destructed and not used for a while, the worker threads will be active in a busy waiting loop. In this case it may be useful to ”pause” the threads until the parallel-for pattern is used again. To attain this, the threadPause method can be used. The next time the parallel-for is used, the non-blocking run-time will be still active.

Another interesting option of the ParallelFor object, is the possibility to switch between two distinct run-time support for the scheduling of loop iterations:

1.

active scheduling where an active non-blocking scheduler thread (the farm’s Emitter) is used to implement the auto-scheduling policy;

2.

passive scheduling where workers cooperatively schedule tasks via non-blocking synchronisations in memory.

Which one is better ? It is difficult to say, as it depends on many factors: parallelism degree, task granularity and underlying platform, among others. As a rule of thumb, on large multi-core and with fine-grain tasks active scheduling typically runs faster; on the other hand, when there are more threads than available cores the passive scheduler allows reduction of CPU conflicts obtaining better performance.

By default, if the number of active workers is less than the number of available cores, than the active scheduling is used. To dynamically switch between active (false) and passive (true) scheduling strategies the disableScheduler method can be used.

4.2.2 ParallelForReduce

The FastFlow ParallelForReduce is used to perform a parallel-for computation plus a reduction operation (by using a combiner function named reduceF in the following) over a sequence of elements of type T. In order to deterministically compute the result, the reduction function needs to be associative and commutative.

The constructor interface is:

where the template type T is the type of the reduction variable, the first parameter sets the maximum number of worker threads that can be used in the ParallelForReduce, the second argument sets non-blocking run-time.

The ParallelForReduce class provides all the parallel-for methods already provided by the ParallelFor class and a set of additional parallel_reduce methods:

The reduceF function specified in all parallel_reduce methods, executes the reduction operation.

As an example, let’s consider the simple case of the sum of an array’s elements:

in this simple test, we used a parallel-for for initialising the array A, and 3 parallel_reduce calls for computing the final sum (the reduction variable) using the default static scheduling, the static scheduling with interleaving and the dynamic scheduling, respectively.

4.2.3 ParallelForPipeReduce

The ParallelForPipeReduce uses a different skeleton implementation of the ParallelForReduce pattern. The ParallelForPipeReduce computes a map function and a sequential reduce function in a pipeline fashion.

This pattern is useful in cases in which the reduce function has to be computed sequentially, for example because there are concurrent write accesses in some memory locations (so they have to be serialised using a lock), or because the reduction operator is not fully commutative. In these cases, the typical solution is to execute the map part (for example using a parallel-for) and then when the map is completed, execute the reduce part sequentially and this may be expensive because a full barrier (between the map and the reduce) is required. The ParallelForPipeReduce pattern allows execution of the map and reduce part in pipeline without any barriers.

The ParallelForPipeReduce pattern is more complex to use than the ParallelForReduce pattern because it requires to explicitly send the tasks to the reduce stage inside the body of the map function. The ParallelForPipeReduce class defined in the parallel_for.hpp file provides only 2 parallel-for methods:

As an example, let’s consider the same simple case implemented in the previous section, i.e. the computation of the sum of array’s elements:

4.2.4 ff_map

The FastFlow map parallel pattern is implemented as an ff_node abstraction and a ParallelForReduce pattern. The idea is that, the map pattern is just an interface to a parallel-for on multi-core platforms, while it provides a simple abstraction for targeting multi-GPGPUs (both OpenCL and CUDA) and, in the future versions, FPGAs on many-core platforms.

Since the ff_map pattern is an ff_node, it may be used as a pipeline stage and as a farm worker.

in the above test, we have a pipeline of two stage, the first stage is a task-farm having two workers defined as map, the second stage is a map. The farm’s workers initialise and generate in the output stream pairs of vector, the single pair of vector is summed in the second stage.

Why use the ff_Map instead of using directly a ParallelFor in a sequential ff_node? The big difference is only in the fact that in case of ff_Map the run-time knows that the ff_node is internally parallel whereas if the parallel-for is used inside the svc method of a sequential ff_node this information is completely transparent to the FastFlow run-time thus not allowing any kind of optimisation (as for example, removing the scheduler or applying a better thread-to-core mapping).

4.3 Examples

4.3.1 Matrix multiplication

Let’s consider the standard ijk matrix multiplication algorithm. We have three nested loops that can be potentially parallelised (note that the internal k-loop is not a plain parallel for loop). In the following code we apply the ParallelFor pattern to the outermost loop (i-loop).

4.3.2 Dot product

The ”dot” product is a simple example of a map pattern combined with a reduction operation. The map is the initial pair wise multiplication of vector elements, and the reduction is the summation of the results of that multiplication.

More formally, given two arrays A and B each with n elements, the dot product A × B is the resulting scalar given by ∑ _i=0^n-1A[i] × B[i].

4.3.3 Mandelbrot fractal

A Mandelbrot set M, is defined by the set of complex numbers c such that:

where

A point c belongs to the Mandelbrot set if and only if:

The following program, which uses the ParallelForPipeReduce pattern for both computing the set line by line (Map part) and for displaying the line just computed (Reduce part), displays the Mandelbrot set in a X window. The result is shown in Fig 4.1.

---

---

4.3.4 Sobel filter

---

---

Let’s consider a very simple usage example in which the ff_map is used as pipeline stage for computing the Sobel filter (see Fig. 4.2) on a stream of input images. The first stage reads image from disk, allocates memory and then sends a task to the second stage (the Map one) which computes the Sobel filter in parallel using a parallel-for. Finally the image is written into the local disk. In the following code we used OpenCV¹ for reading and writing images and for converting them to grayscale.

Chapter 5
Data-flow parallelism

The data-flow programming model is a general approach to parallelization based upon data dependencies among a program’s operations. Its theoretical and methodological value is quite fundamental in parallel processing.

The computations is expressed by the data-flow graph, i.e. a DAG whose nodes are instructions and arcs are pure data dependencies.

---

---

If instead of simple instructions, portions of code (sets of instructions or functions) are used as graph’s nodes, then it is called the macro data-flow model (MDF). The resulting MDF program is therefore represented as a graph whose nodes are computational kernels and arcs read-after-write dependencies. It is worth noting that, the data-flow programming model is able to work both on stream of values and on a single value. For this reason, it is considered somehow a primitive model of computation.

5.1 The ff_mdf data-flow skeleton

The mdf skeleton in FastFlow calles ff_mdf implements the macro data-flow parallel pattern. The run-time of the FastFlow mdf pattern is responsible for scheduling fireable instructions (i.e. those with all input data dependencies ready) and managing data dependencies.

Currently, the internal implementation of the FastFlow mdf pattern is a 2-stage pipeline, the first stage is responsible for dynamically generating the graph instructions by executing the users’ code, and the second stage (a task-farm with feedback channel) is responsible for managing task dependencies and task scheduling. In the next version of FastFlow, other different implementations using less resources will be provided to the users.

Creating graph tasks

In order to show how to use the mdf pattern, let’s take a look at the following simple case. Suppose you have the following sequential code:

here we can identify 4 macro instructions that can be executed concurrently with the FastFlow mdf pattern by specifying, for each instruction, which are the input or output parameters of the function that has to be executed (in this case sum2 and sum3). For example, the first instruction in the code above has two input parameters (A and B) and one output parameter (C) that have to be passed to the function sum2. A parameter is provided to the run-time as param_info type, which has two fields, one is the pointer of the input or output of the ”real” parameter and the second is the ”direction” which can be INPUT,OUTPUT or VALUE (this last one is used mainly for those parameters that can be evaluated as a single value, do not constitute a real dependency). The function and the parameters are passed to the run-time using the AddTask method of the mdf class. The resulting code is the following one:

5.2 Examples

In this section we propose two numerical application: the block-based matrix multiplication and the block-based Cholesky factorisation.

5.2.1 Block-based matrix multiplication

As a more complex usage example of the FastFlow mdf pattern we consider here the block-based matrix multiplication algorithm. The algorithm is sketched in Fig. 5.2.

This version computes in parallel the C_ij blocks doing p-passes. A more cache-friendly implementation can be implemented.

---

---

5.2.2 Block-based Cholesky factorisation

To be added

Bibliography